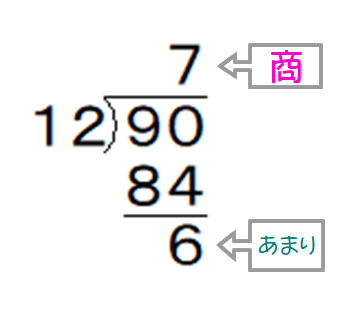
中央値を求めるためには、資料を大きさ順に並べ替えます。 資料の個数が奇数の場合 このように真ん中に位置する資料の値が中央値となります。 一方、資料の個数が偶数の場合 真ん中にある値を1つに決められません。 そのため、真ん中にある2つの
数学 言葉- 数学の教科書において「自明」「明らか」といった言葉は頻出でありながら、本文でその意味がちゃんと説明されることは稀で、結果としてそれらの言葉を 誤解 している人や、それらの言葉が使われることに 圧力・反感 を感じる人も一定の割合でいるようです。 数学は言葉 一般の人が、数学を本を読んで理解しようとするとき、二つの障壁を乗り越えねばならない。 一つは、語られている概念が抽象的であること、そしてもう一つは、それを語っている「言葉」が数式というこれまた「読みにくい言語」だ、ということだ。 書き手が後者を突破する道は二者択一である。 第一の道は、数式を使わず、極力日常の言語
数学 言葉のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 | ||
 |  |  |
 |  |  |
「数学 言葉」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「数学 言葉」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
 |  |  |
「数学 言葉」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
 |  |  |
「数学 言葉」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「数学 言葉」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「数学 言葉」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 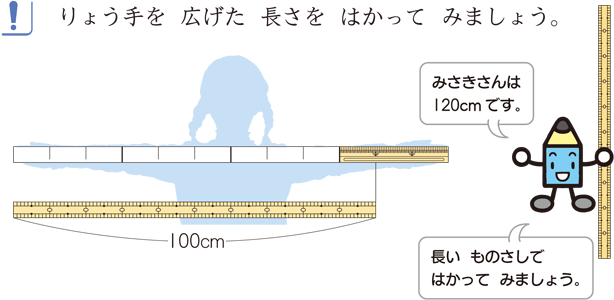 |
 |  | |
 |  | |
 |  | |
「数学 言葉」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  | |
「数学 言葉」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |
答えは「36メートル差」です。 「勝者が走り終えた瞬間に、敗者は80メートル地点を走っていた」ということが分かります。 しかし、常にメートル差で走り続けていたわけではなく「ゴールした瞬間の差」であることから、スタート後に少しずつ差がついたことが判明します。 A・Bがそれぞれ100メートルを完走した瞬間に、敗者は勝者の80%の距離を走ったことが数学 4000年の歩み 上野 健爾 はじめに 数学と聞くと、いやな思いをされる方が多いよう です。これは、数学がテストを通して選別の道具と して使われてきた結果、数学の内容の面白さよりも テストの成績だけに関心が向かう結果だと思われま す。





0 件のコメント:
コメントを投稿